BCurve2D / BCurve3D

These two classes represent Bezier curves in 2D and 3D space respectively. The API for both classes is the same so they are discussed here together. If you have never come accross Bezier curves before then you might read this Wikipedia article.

The Bezier curve that most people first discover is the cubic Bezier curve. This curve has 4 control points, the curve passes thorugh the first and the last point, and its shape is controlled by the two intermediate points. What many people don't realise is that a Bezier curve can have any number of intermdiate points giving the curve a more complex shape but still smooth.

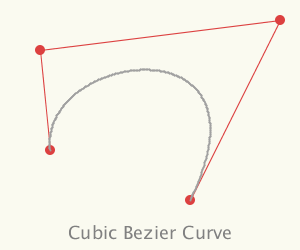
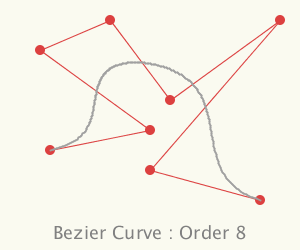
In the above pictures the control points are shown as red dots and the red lines link them in the order thay were specified. The minimum number of controls points is 2 (a straight line) but there is no upper limit to the number of control points you can pass to these classes.

Creating the Bezier path

BCurve2D(float[][] points, int nbrSlices)
BCurve2D(PVector[] points, int nbrSlices)

BCurve3D(float[][] points, int nbrSlices)
BCurve3D(float[][] points, int nbrSlices, PathOrthogonal ortho)

BCurve3D(PVector[] points, int nbrSlices)
BCurve3D(PVector[] points, int nbrSlices, PathOrthogonal ortho)

float[][] points

PVector[] points

nbrSlices

ortho